计数排序(Counting Sort)是时间复杂度为O(n)的排序
前言
排序算法是每个程序员应该掌握的。
适用范围
待排序的元素在某一个范围[MIN, MAX]之间。
计数排序只适合元素是整数,小规模的排序。
空间复杂度
计数排序需要一个辅助空间,空间大小为O(MAX-MIN),用来存储所有元素出现次数(计数)。
计数排序的核心是,空间换时间。
关键步骤
- 扫描待排序数据arr[N],使用计数数组counting[MAX-MIN],对每一个arr[N]中出现的元素进行计数
- 扫描计数数组counting[],还原arr[N],排序结束
举个例子
假设待排序的数组,
arr={5, 3, 7, 1, 8, 2, 9, 4, 7, 2, 6, 6, 2, 6, 6}
很容易发现,待排序的元素在[0, 10]之间,可以用counting[0, 10]来存储计数。
第一步: 统计计数
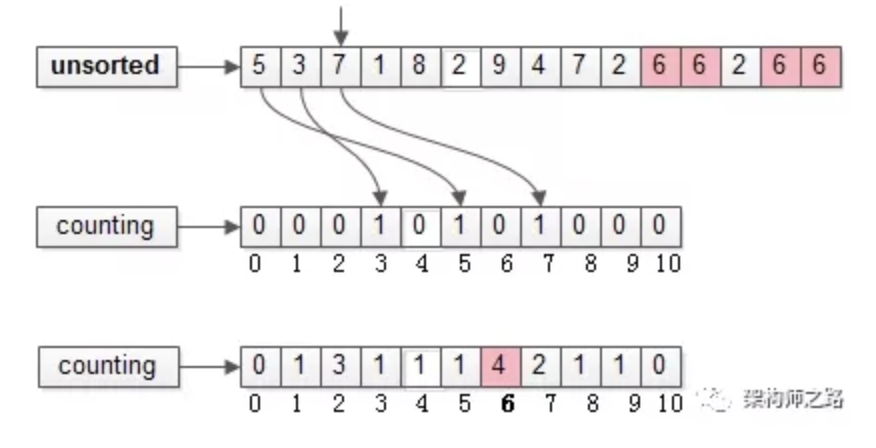
扫描未排序的数组arr[N],对每一个出现的元素进行计数。
扫描完毕后,计数数组counting[0, 10]会变成上图中的样子。
如粉色示意,6这个元素在arr[N]中出现了4次,在counting[0, 10]中,下标为6的位置计数是4。
第二步: 还原数组
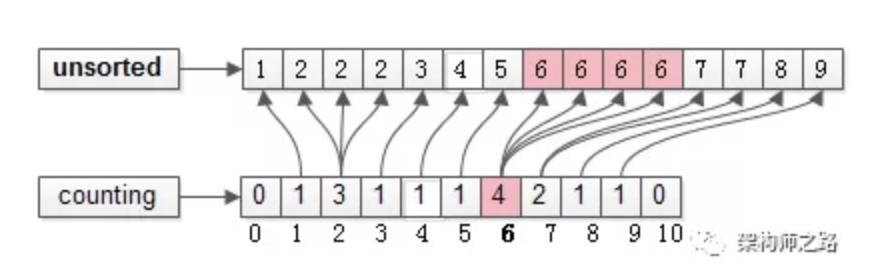
扫描计数数组counting[0, 10],通过每个元素的计数,还原arr[N]。
如上图粉色示意,count[0, 10]下标为6的位置计数是4,排完序是4个连续的6。
从counting下标MIN到MAX,逐个还原,填满arr[N]时,排序结束。
总结
计数排序,时间复杂度为O(n)。
当待排序元素个数很多,但值域范围很窄时,计数排序是很节省空间的。
计数排序只适合元素是整数,小规模的排序。
参考链接