基数排序(Radix Sort)是时间复杂度为O(n)的排序
前言
时间复杂度为O(n)的排序,常见的有三种:
基数排序(Radix Sort)
计数排序(Counting Sort)
桶排序(Bucket Sort)
计数排序->桶排序->基数排序,三者的排序思想是相通的,是逐渐复杂,使用性更广的。
基数排序分为两类:
- 最低位优先法,简称LSD法
- 最高位优先法,简称MSD法
适用范围
整数、字符串。
空间复杂度
O(n)
关键步骤
LSD 先从最低位开始排序,再对次低位排序,直到对最高位排序后得到一个有序序列。
两个关键要点:
(1) 基: 被排序的元素的“个位”“十位”“百位”,暂且叫“基”;
(2) 桶: “基”的每一位,都有一个取值范围,例子中“基”的取值范围是0-9共10种,所以需要10个桶(bucket),来存放被排序的元素;
LSD 步骤为:
FOR (每一个基) {
//循环内,以某一个“基”为依据
第一步:遍历数据集arr,将元素放入对应的桶bucket
第二步:遍历桶bucket,将元素放回数据集arr
}
举个例子
假设待排序的数组arr={72, 11, 82, 32, 44, 13, 17, 95, 54, 28, 79, 56}

例子中“基”的个数是2(个位和十位), 所以 FOR循环会执行两次。
【第一次:以“个位”为依据】
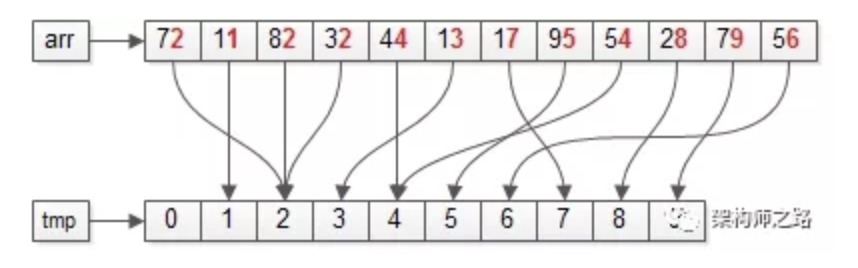
上图中标红的部分,个位为“基”。
第一步:遍历数据集arr,将元素放入对应的桶bucket;
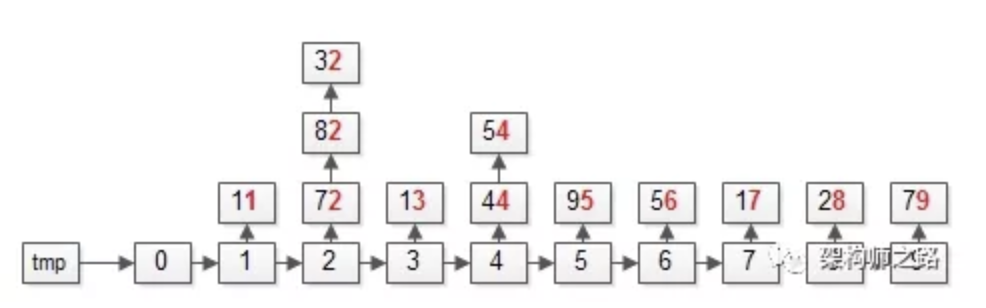
操作完成之后,各个桶会变成上面这个样子,即:个位数相同的元素,会在同一个桶里。
第二步:遍历桶bucket,将元素放回数据集arr;需要注意,先入桶的元素要先出桶。
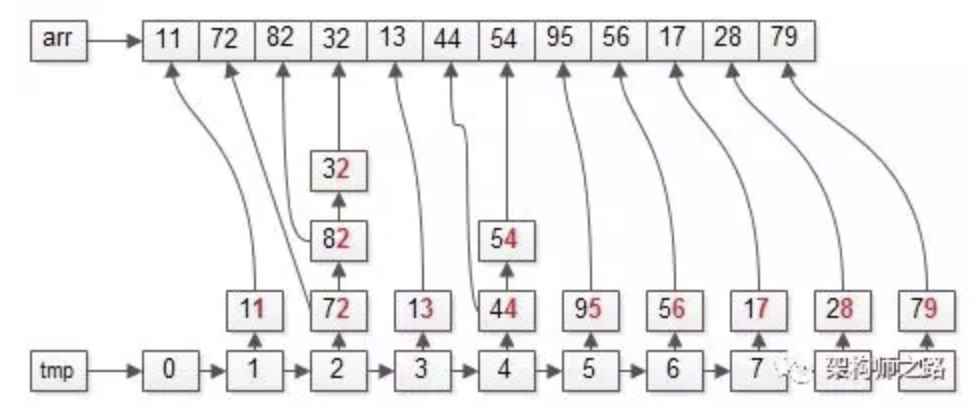
操作完成之后,数据集会变成上面这个样子,即:整体按照个位数排序了, 个位数小的在前面,个位数大的在后面。
【第二次:以“十位”为依据】
上图中标红的部分,十位为“基”。
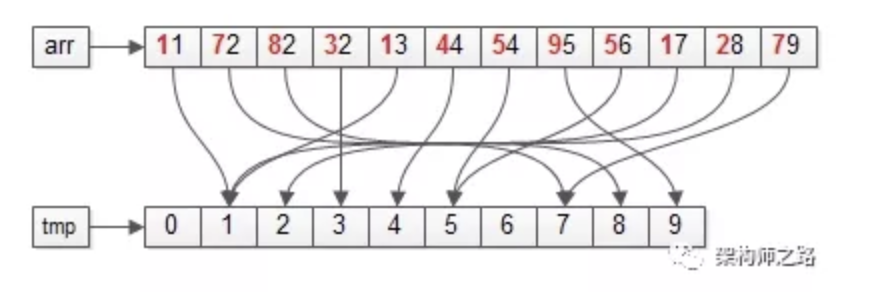
第一步:依然遍历数据集arr,将元素放入对应的桶bucket;
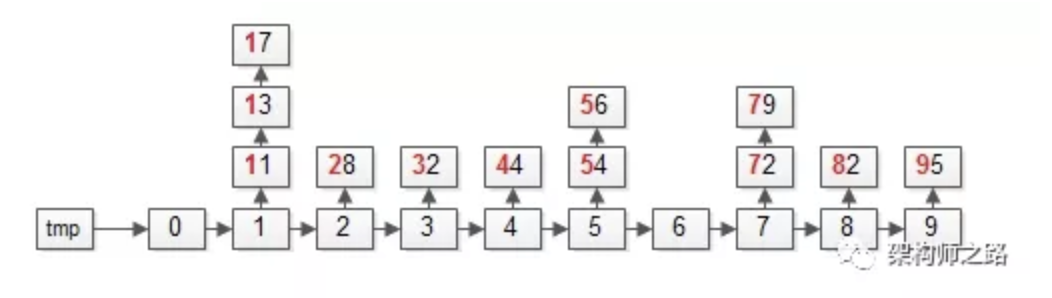
操作完成之后,各个桶会变成上面这个样子,即:十位数相同的元素,会在同一个桶里。
第二步:依然遍历桶bucket,将元素放回数据集arr;
操作完成之后,数据集会变成上面这个样子,即:整体按照十位数也排序了。
十位数小的在前面,十位数大的在后面。
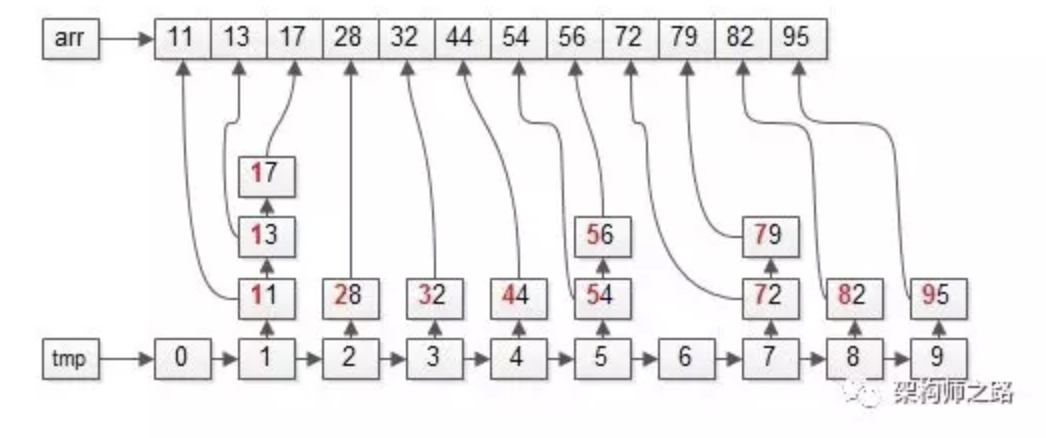
首次按照个位从小到大,第二次按照十位从小到大,即:排序结束。
MSD 与LSD相反,从高位向地位开始比较,是由高位数为基底开始进行分配,
但在分配之后并不马上合并回一个数组中,
而是在每个“桶子”中建立“子桶”,
将每个桶子中的数值按照下一数位的值分配到“子桶”中,在进行完最低位数的分配后再合并回单一的数组中。
举个例子
假设待排序的数组arr={15, 25, 105, 78, 34, 21, 32, 41}
从最高位百位依次入桶,只有105有百位,其他百位按0算;
检测每个桶中的数据。当桶中的元素个数多于1个的时候,要对这个桶递归进行下一位的分组。
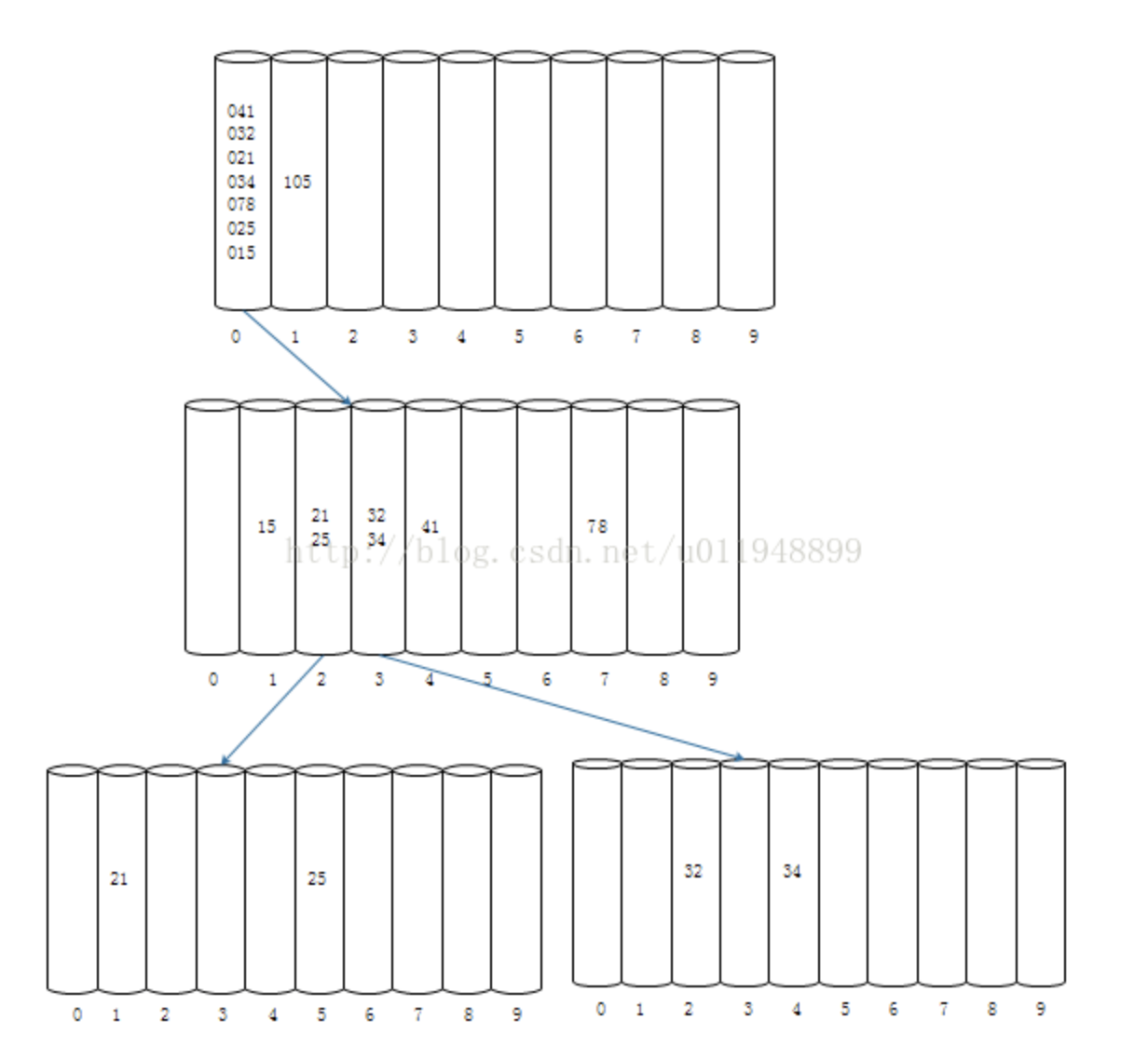
如果使用词典排序来对可变长度整数表示进行排序,则从1到10的数字的表示将被输出为1,10,2,3,4,5,6,7,8,9,
如同较短的按键左对齐,并在右侧用空白字符填充以使短按键与最长按键一样长,以确定排序顺序。
总结
基的选取,可以先从个位开始,也可以先从十位开始,结果是一样的;
基数排序,是一种稳定的排序;
时间复杂度,可以认为是线性的O(n);
参考链接